On cherche à déterminer les valeurs du triangle de Pascal (Figure 1).

Dans le triangle de Pascal, chaque ligne commence et se termine par le nombre 1. Comme l’illustre la Figure 2, on additionne deux valeurs successives d’une ligne pour obtenir la valeur qui se situe sous la deuxième valeur.

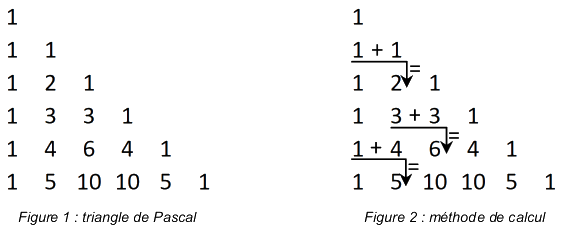
Compléter les fonctions ligne_suivante et pascal ci-dessous. La fonction ligne_suivante prend en paramètre une liste d’entiers ligne correspondant à une ligne du triangle de Pascal et renvoie la liste correspondant à la ligne suivante du triangle de Pascal. La fonction pascal prend en paramètre un entier n et l’utilise pour construire le triangle de Pascal ayant n+1 lignes sous la forme d’une liste de listes.

def ligne_suivante(ligne):
    '''Renvoie la ligne suivant ligne du triangle de Pascal'''
    ligne_suiv = [...] 
    for i in range(...): 
        ligne_suiv.append(...) 
    ligne_suiv.append(...) 
    return ligne_suiv

def pascal(n):
    '''Renvoie le triangle de Pascal de hauteur n'''
    triangle = [ [1] ]
    for k in range(...): 
        ligne_k = ... 
        triangle.append(ligne_k)
    return triangle

Exemples:

>>> ligne_suivante([1, 3, 3, 1])
[1, 4, 6, 4, 1]
>>> pascal(2)
[[1], [1, 1], [1, 2, 1]]
>>> pascal(3)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1]]